일의 양 역학적 관점에서 힘 F가 물체 A의 변위 방향과 같은 방향으로 작용했다면 그 힘은 물체 A에 대하여 양(+)의 일(positive work)을 했다고 말하며 힘 F의 방향과 물체 A의 변위 방향이 반대일 때 그 힘은 물체 A에 대하여 음(-)의 일(negative work)을 했다고 말한다.
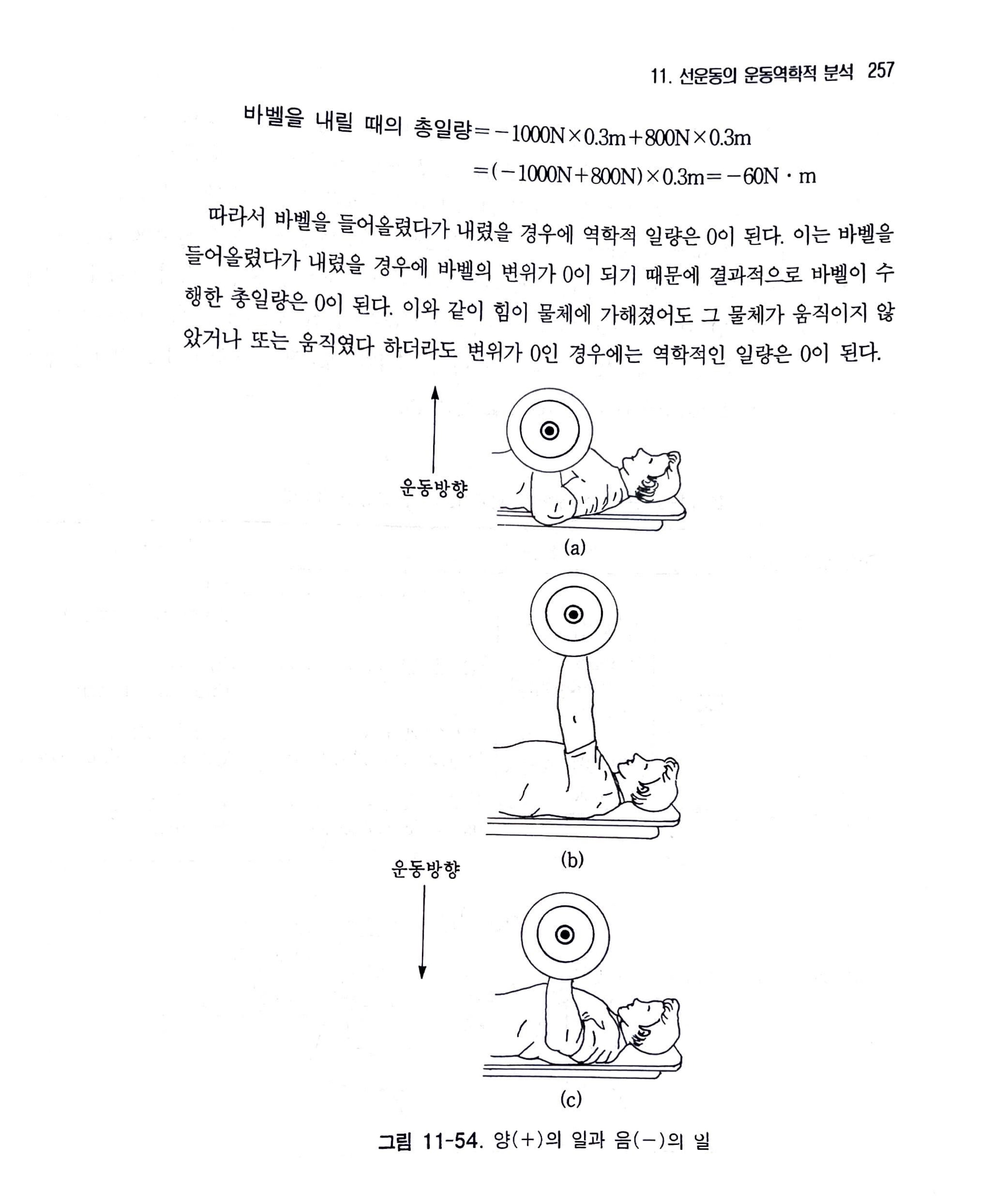
그림 11-54와 같이 바벨을 가지고 벤치 프레스를 할 경우에 바벨을 들어 올릴 때(그림 11-54의 (a))는 +의 일을 하게 되며 팔을 쭉 뻗쳐 정지된 상태에서 바벨을 지탱하고 있을 때(그림 11-54의 (b))는 일을 하지 않고 있는 상태(W=0)이며, 바벨을 내릴 때(그림 11-54의 (c))는 -의 일을 하게 된다. 이와 같이 역학적인 일(mechacical work)의 양은 힘의 작용 방향과 물체의 변위 방향에 따라 +, -0, -의 세 가지 경우로 나누어질 수 있다.
그림의 (a)에서 바벨을 0.3m 들어올리는데 1000N의 근력이 수직상방으로 가해졌다면 바벨의 이동 방향과 근력의 작용 방향이 동일하므로 근력은 300N * m (W=1000N * 0.3m)의 양(+)의 일을 수행한 것이 된다. 그러나 그림의 (c)와 같이 바벨을 들어 올린 거리만큼 다시 내릴 때는 근력이 수직상방으로 가해지는 반면에 바벨의 변위는 수직하방이므로 근력이 행한 일의 양은 -300N * m (W=-1000N * 0.3m)가 된다.
그러나 실제의 일량은 이에 부과하여 바벨을 올리거나 내릴 때에 작용하는 중력의 작용을 고려해야 한다. 예를 들어 무게가 800N인 바벨을 0.3m 들어올린 경우에 총일량은 실시자가 수직상방으로 발휘한 근력에 의한 일량과 중력에 의하여 바벨에 수직하방으로 작용한 바벨 자체의 무게에 의한 일량의 합으로 나타내야만 한다.
바벨을 들어 올릴 때의 총일량
= 실시자의 근력에 의한 일량 + 바벨 무게에 의한 일량
= 1000N * 0.3m - 800N * 0.3m
=(1000N - 800N) * 0.3m = 60N * m 바벨을 내릴 때의 총일량
= -1000N * 0.3m + 800N * 0.3m
= (-1000N + 800N) * 0.3m = -60N * m 따라서 바벨을 들어올렸다가 내렸을 경우에 역학적 일량은 0이 된다. 이는 바벨을 들어올렸다가 내렸을 경우에 바벨의 변위가 0이 되기 때문에 결과적으로 바벨이 수행한 총일량은 0이 된다. 이와 같이 힘이 물체에 가해졌어도 그 물체가 움직이지 않았거나 또는 움직였다 하더라도 변위가 0인 경우에는 역학적인 일량은 0이 된다. 앞서 언급한 바와 같이 인체의 근력이 수행한 일은 +, 0, -의 세 가지 경우로 구분되는데 이는 골격근의 근수축 형태와 밀접한 연관이 있다. 근육의 수축 형태는 표 11-8과 같이 근육의 길이가 변하지 않는 등척성 수축과 근육의 길이가 변하는 등장성 수축의 두 가지 경우로 크게 구분된다. 그리고 등장성 수축은 발휘 근력이 외력보다 커서 근육의 길이가 짧아지는 단축성 수축과 발휘 근력이 외력보다 작아서 근육의 길이가 피동적으로 길어지는 신장성 수축으로 세분된다. 등척성 수축시 발휘 근력이 행한 역학적 일은 0이기 때문에 역학적 일은 등장성 수축에 의한 발휘 근력에 의해 수행됨을 알 수 있다. 그런데 바벨을 들어올리는 경우와 같이 근력의 작용 방향과 근 수축 방향이 동일한 단축성 수축시에는 양(+)의 일을 수행하게 되며 바벨을 내리는 경우와 같이 근력의 작용 방향과 근 수축 방향이 반대인 신장성 수축시에는 음(-)의 일을 수행하게 된다. 예를 들어 팔굽혀 펴기는 상지 근육군의 단축성 수축과 신장성 수축이 반복되는 운동으로 상지 근육군이 단축성 수축(팔꿈치가 신전될 때)때는 양(+)의 일을 하게 되며 신장성 수축(팔꿈치가 굴곡될 때)때는 음(-)의 일을 하게 된다.



<생체역학>, 예종이, 태근, p256
'체육 > 운동역학' 카테고리의 다른 글
| [운동역학] 높이뛰기에 적용된 역학적 원리 (0) | 2021.10.07 |
|---|---|
| [운동역학] 형태항력 - 사이클 1인자는 2인자 자리를 좋아하더라 (0) | 2021.10.06 |
| [운동역학] 10m 플랫폼 다이빙 동작에 대한 운동역학적 분석 (0) | 2021.09.27 |
| [운동역학] 운동학적(kinematic) 변인과 운동역학적(kinetic) 변인 (0) | 2021.08.30 |
| [운동역학] 항력이 야구공, 테니스공, 골프공의 비행에 미치는 영향 / 베르누이 정리 / 마그누스 효과 (0) | 2021.08.06 |
